Aritmetika dan Geometri

Deret hitung atau deret aritmetika adalah urutan bilangan di mana bilangan berikutnya merupakan “penambahan atau pengurangan” bilangan sebelumnya dengan suatu bilangan beda tertentu.

Deret ukur atau deret geometri adalah urutan bilangan di mana bilangan berikutnya merupakan “perkalian atau pembagian” bilangan sebelumnya dengan suatu bilangan beda tertentu.

Misalnya,

2, 5, 8, 11, 14, 17, ... (ditambah)
20, 15, 10, 5, ... (dikurang)
Deret bilangan diatas merupakan deret aritmatika karena pola bilangan berikutnya merupakan hasil  “ditambah 3” dan “dikurang 5” dari bilangan sebelumnya.

3, 6, 12, 24, 48, 96, ... (dikali)
200, 100, 50, 25, ... (dibagi)
Deret bilangan diatas merupakan deret aritmatika karena pola bilangan berikutnya merupakan hasil  “di kali 2” dan “di bagi 2” dari bilangan sebelumnya.

1. Aritmatika

Suku ke-n (Un)

dengan
a = U1 = suku pertama
b = beda
Un = suku ke-n

Jumlah suku ke-n (Sn)

Suku ke-n (Un) bila Sn diketahui

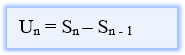
Suku tengah (Ut)

Jika diantara dua suku barisan aritmatika disisipkan k buah suku sehingga membentuk barisan aritmatika baru maka beda barisan aritmatika setelah disipkan k buah suku akan berubah.

b’ = beda barisan yang baru
k = banyak suku yang disisipkan

Banyak suku dari barisan aritmatika yang disisipkan k buah suku juga akan berubah.

n’ = banyak suku barisan aritmatika baru

Contoh :

10, 20, 30, 40, 50, 60, ...
Diantara setiap dua suku bilangan diatas akan disisipkan 4 buah bilangan sehingga bilangan-bilangan semula dengan bilangan-bilangan yang disisipkan membentuk barisan aritmatika baru. Carilah beda dari barisan aritmatika yang terbentuk.

Jawab :
Jumlah beda awal (b) = U2 – U1 = 20 – 10 = 10
Setelah disisipkan, maka barisan bilangannya akan berpola seperti ini
10, a, b, c, d, 20, e, f, g, h, 30, i, j, k, l, 40, m, n, o, p, 50, q, r, s, t, 60 ...
Maka, untuk mendapatkan barisan aritmatika yang baru, beda baru (b’) adalah b/(k+1) = 10/(4+1) = 10/5 = 2.

2. Geometri

Rasio

Suku ke-n

Jumlah suku ke-n

Suku tengah (Ut)

Jika diantara dua suku barisan aritmatika disisipkan k buah suku sehingga membentuk barisan geometri baru maka rasio barisan geometri setelah disipkan k buah suku akan berubah.

Banyak suku dari barisan aritmatika yang disisipkan k buah suku juga akan berubah.

Deret geometri tak berhingga

Deret geometri tak berhingga merupakan deret yang memiliki banyak suku yang tak berhingga.

r dengan syarat -1< r <1

Contoh Soal :

1. Seorang anak bernama Intan memiliki sebuah pohon jati yang mengalami pertambahan tinggi per hari 1/8 kali dari tinggi sebelumnya. Pohon tersebut diukur seminggu sekali. Jika tinggi pohon jati 23 cm pada pengukuran awal, maka berapakah tinggi pohon jati pada pengukuran berikutnya ?

1. 16,1 cm
2. 49,05 cm
3. 52,45 cm
4. 50,07 cm
5. 32,2 cm

Jawab :

2. Sebuah bola dijatuhkan ke lantai dari ketinggian 2 meter. Setiap kali setelah memantul, bola itu mencapai ketinggian tiga perempat dari ketinggian yang dicapai sebelumnya. Panjang lintasan bola tersebut dari pantulan ketiga sampai berhenti adalah ... meter.

1. 3,38
2. 4,26
3. 5,50
4. 6,75
5. 8,00

Jawab :

bila kita memantulkan sebuah bola, maka bola tersebut akan naik dan kemudian turun dengan tinggi yang sama pula, lalu pada pantulan berikutnya akan semakin menurun, sehingga panjang lintasan totalnya adalah 2 kali (naik dan turun), sehingga panjang lintasan total pada soal diatas adalah S∞ = 27/8  x 2 = 27/4 = 6,75 meter.

3. Diketahui jumlah n bilangan positif genap yang pertama adalah 272. Dari bilangan-bilangan genap tersebut, jumlah lima bilangan terakhirnya adalah ...

1. 150
2. 140
3. 130
4. 120
5. 110

Jawab :

Subscribe to receive free email updates: